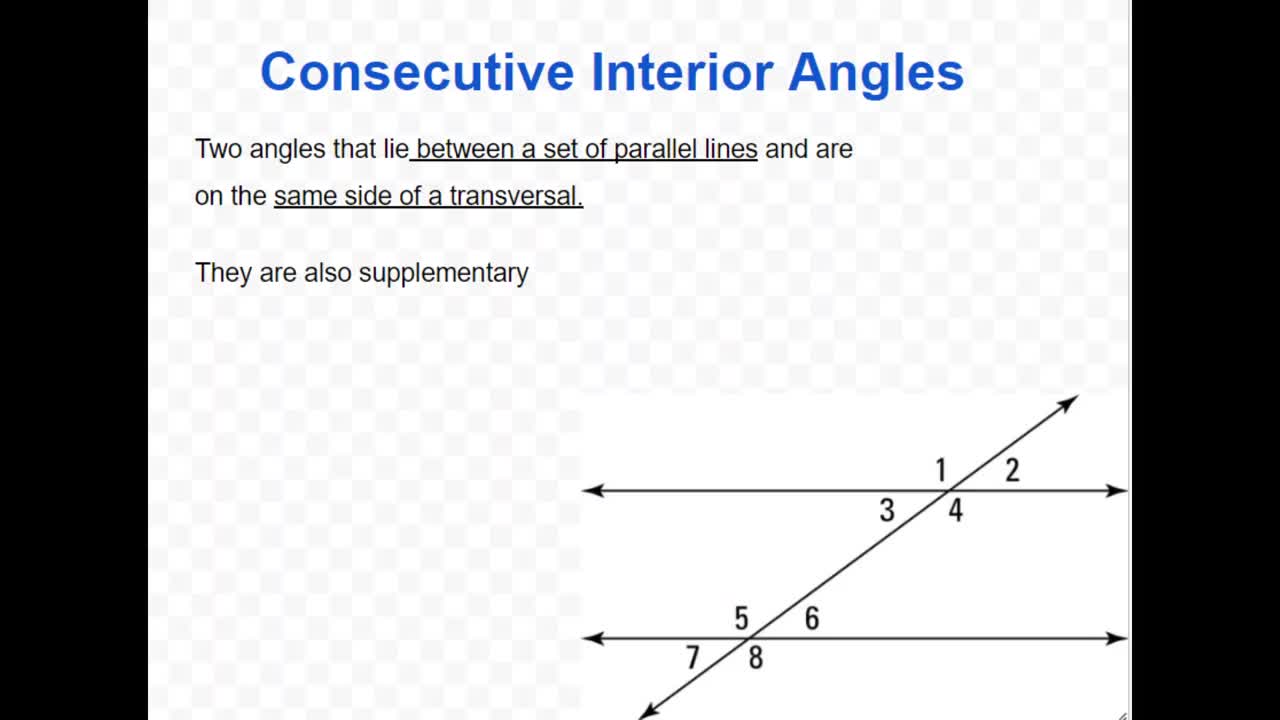
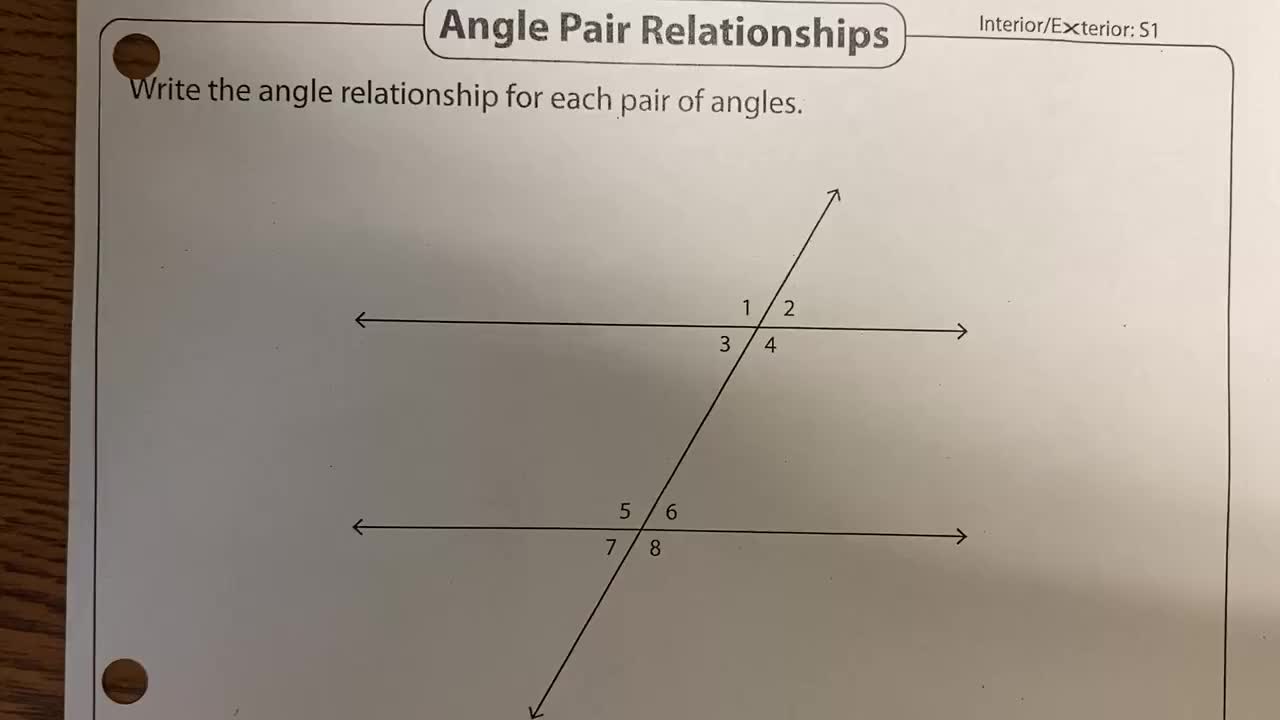
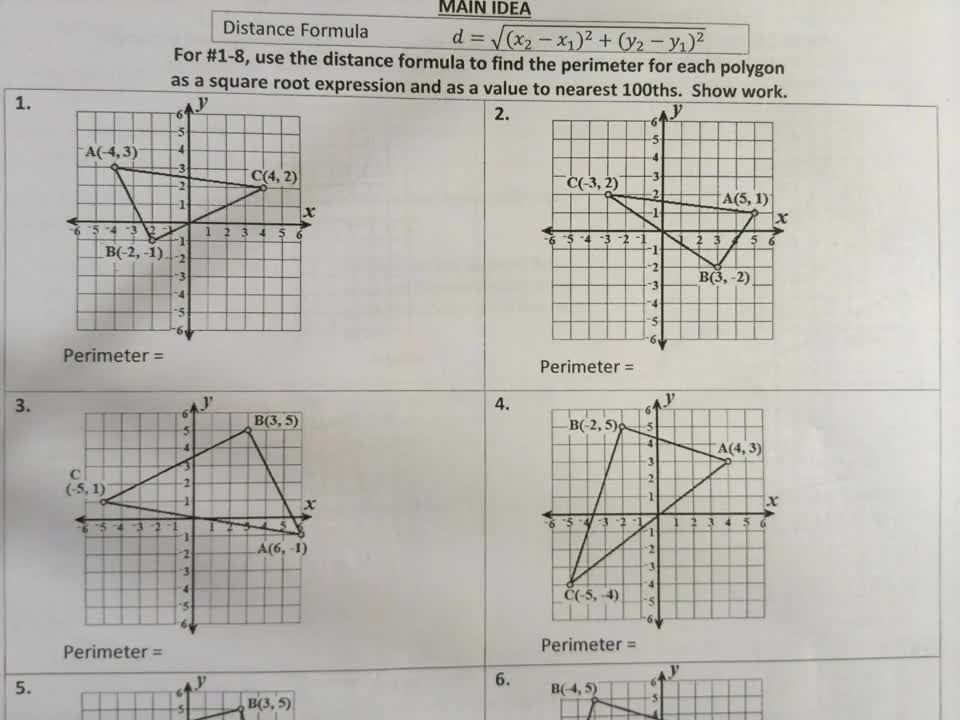
Middle School > Math > Geometry Videos
A very well-known principle in geometry is the Pythagorean theorem. It states that the sum of the squares of the two shorter sides of a right triangle is equal to the square of its longer side. Put into an equation, that’s c2= a2+b2, where a and b are the lengths of the shorter sides (or the sides that form the right angle) and c is the length of the longest side (or the hypotenuse). At first glance, it may seem like just a normal mathematical formula, but in reality, it has many different uses.
In architecture, the Pythagorean theorem can be used to calculate the length of a diagonal line that connects the ends of two straight lines that are perpendicular to each other. This is useful in building, say, the roof of a house. If the length and the height of the roof is given, the architect can calculate the length of the diagonal portion of the roof. In turn, he would know how much material and in what dimensions they should be in to properly put up the roof.
The theorem is also useful in navigation. Say a pilot wants to know the right spot to begin descending towards a runway. He can use his height above ground and the distance to the airport, which are two perpendicular lines, to pinpoint the place where he will begin the plane’s descent. This is important because the plane has to be tilted at an angle that is not so steep, allowing the landing to be smooth.
Because the theorem has a number of real-world applications, it is one thing that students of math should master. It’s a very simple principle, and the formula makes it also easy to remember. Once students know how to use it, they will find more practical applications for the theorem themselves.